Scheduling workshops with algorithms

At Criteo R&D, we have an off-site summit every year where the whole dev-team is invited to a nice location for a couple of days, for learning, fun activities and networking with various R&D teams.

During last year’s event, there were series of workshops by various people from our R&D, where they would talk about something (remotely) related to their job at Criteo, like how catalog import works, what is an agent-based model, or why the B-17 Flying Fortress is an example of great project management. There was 37 such workshops, to be distributed over 5 time-slots, that’s 551090558931404263200 different combinations (how I got this number is left as an exercise for the reader). The problem is : how do you schedule those workshops to make everyone happy ?

The first solution is to just throw them randomly and hope for the best, but that doesn’t really help in making people happy. Another solution is to have someone workshops, apply intuition and try to schedule them in a way that can satisfy everyone, but at Criteo we know best that humans are usually bad at this kind of task. A third solution is to have people answer a quick survey, and “someone” write a program eating the survey’s results and spit out an optimal good enough schedule. That “someone” being me.

So we asked everyone in our R&D to read through workshops’ abstracts, and rank their top 8. From this, I got a file with 255 answers, one line per person, and 8 numbers corresponding to the top 8 workshops people would like to attend. Or at least something close to that, since :

• Some people only filled 2 or 3 workshops.
• Some people only filled the bottom of their top 8. I manually realigned them as their top.
• Reading through the list of workshops, I realized some people were giving several workshops, I had to make sure not to schedule them at the same time.
• People giving workshops would have to attend their own workshop, making it de facto their #1 choice even though they didn’t list it in their preferences.

To start working on this data set, I needed a way to evaluate a solution. I started with the assumption that people would always go to the workshop that was ranked highest in their choices. Then, I decided to assign a “happiness” value function to workshops, giving a score that would be granted only if the person assists to the workshop. I arbitrarily chose an exponentially decreasing function exp(-2*rank/nb_choices) plotted below :

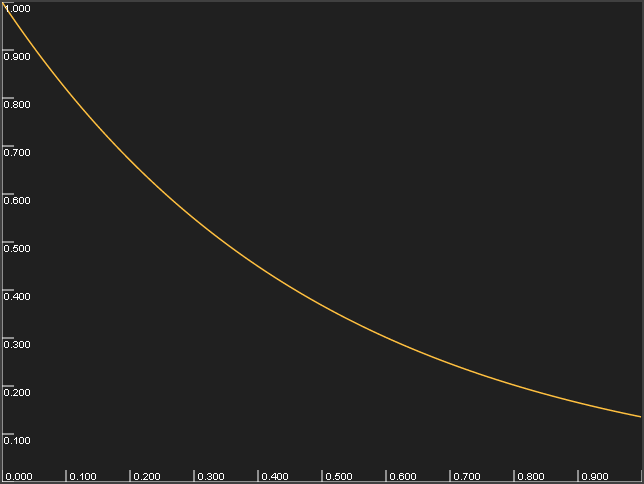
Figure showing the happiness value

Choice #1 would always have a score of 1.0 (rank is zero-based), the last choice would have a score close to exp(-2) ≈ 0.135, and choices in between are spread evenly. The aim is now to maximize this score.

This is nice, but I was a bit sad because this score didn’t mean anything, and I wasn’t very satisfied with it. So I decided to redefine it as an angriness score : participating in a workshop in your top 5 gives zero angriness points because you are expected to be able to attend them. Not being able to assist to your top 5 gives you angriness points as described above, and being able to assist to a workshop you ranked #6 to #8 reduces a bit your angriness of not being able to attend something better. This is equivalent to subtracting the “perfect” score for each person from the previous solution (with negative happiness = angriness), so it doesn’t change much, but rather, it gives a better sense of where we are.

Since I didn’t really know which algorithm to use, and the problem looked NP hard, I decided to use simulated annealing, the tool of champions : I’d pick a random configuration to start with, compute its score, then flip two workshops, compute the score again, and keep the new solution if the score is greater, or if some random value tells me to (so that we don’t get too stuck in local maxima).

I added a few constraints : I had a list of pairs of mutually exclusive workshops (given by the same people), if they happened in the same timeslot, I’d discard the solution and pick a new permutation. Also, we didn’t want a workshop to have no attendees, so after looking a bit at generated solutions for typical numbers, I decided it was ok to discard solutions where a workshop had less than 10 attendees.

After a little bit debugging, I was ready to run this for some time and get a good solution. Since my computer has 8 cores, and I was too tired to parallelize this code, I launched 8 instances of the same program, with different permissiveness parameters for the anealing. I let this run for approximately a full day, and I got a nice scheduling option. As a bonus, I was able to predict how many people would attend a workshop, and this helped dispatch them in the different rooms, some of which were twice the size of others.

As the off-site event took place, most people had forgotten which workshops they had chosen when they ranked their top 8, but their taste didn’t change too much, and everyone was happy. As a colleague made me notice, we could even see some tracks emerge in the scheduling : for instance, machine learning-themed talks were on different time slots so that one could attend all of them. It was great to see my program did its job well !

Input format

on each line is a list of one to nine workshops ID’s separated by commas, indicating the choices of one person. The most wanted workshop is on the left.

the following pairs of workshops are incompatible (i.e. they cannot be in the same time slot) : (2,3),(8,9),(3,28),(27,29),(23,24)

note: there are 37 workshops, with ID’s 1 to 37. We want to schedule them over 5 time slots.

Scoring

happiness(rank, nbChoices) = Math.Exp((-2.0*rank)/nbChoices) rank is zero-based

If someone cannot attend to a workshop in their top five, we subtract the happiness from their score. If they can attend a workshop they ranked 6-9, we add the happiness to their score.

i.e. someone gave as their top (1,2,3,4,5,6,7,8) and can only attend (1,3,4,5,6) because 1 and 2 were in the same time slot, will have a score of -Math.Exp((-2.0*1)/8)+Math.Exp((-2.0*5)/8) = -0.7788 + 0.2865 = -0.4923

Note that a score is always negative (zero means perfect matching).

The total score of a solution is the sum of happiness of all people, divided by the number of people.

Beat me

The solution we used had a score of -0.364466, can you find a better arrangement ?

This solution respects the added constraint that all workshops have at least 10 attendees.